Bernoullijeva jednačina

Bernoullijeva jednačina prikazuje odnos između brzine, pritiska i gustoće tekućine u kretanju. Ona kaže da je u slučaju stabilnog strujanja nestišljive tekućine, bez trenja, ukupna energija tekućine jednaka duž svih presjeka; porastom brzine tekućine pada njen statički pritisak i obratno. Zbir statičkog i dinamičkog pritiska u horizontalnom strujanju daje ukupan pritisak, koji je konstantan u svim presjecima. Drugim riječima, Bernoullijeva jednačina predstavlja zakon očuvanja energije, koji nam u slučaju stacionarnog strujanja tekućine govori da za vrijeme stacionarnog strujanja jedinica mase tekućine (njen diferencijalni dio) ima konstantnu energiju duž cijele strujne cijevi.

Mehanika kontinuuma
|
Zakoni Zakon održanja mase Zakon održanja količine kretanja Zakon održanja energije Nejednakost entropije
Mehanika čvrstih tijela Čvrsta tijela · Napon · Deformacija · Teorija konačnih deformacija · Teorija infinitezimalnih napreazanja · Elastičnost (linearna) · Plastičnost · Savijanje · Hookeov zakon · Teorija o otkazu materijala · Mehanika loma · Mehanika kontakta (frikciona)
Mehanika fluida Fluidi · Statika fluida Dinamika fluida · Arhimedov zakon · Bernoullijeva jednačina · Navier–Stokesove jednačine · Hagen–Poiseuilleova jednačina · Pascalov zakon · Viskoznost (Njutnovski fluid · Nenjutnovski fluid) · Potisak · Pritisak
Naučnici Bernoulli · Boyle· Cauchy · Charles · Euler · Gay-Lussac · Hooke · Newton · Pascal · Navier · Stokes

Odnosno Bernouiiljeva jednačina govori o konstantnosti:

• potencijalne energije ... $\ z+{p \over \rho g}$
  i
• kinetičke energije ... $\ {v^{2} \over 2g}$.

Objašnjenje Bernoullijeve jednačine

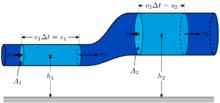
Kroz cijevi različitog presjeka protječe tekućina (slika). Okomito na smjer strujanja postavljene su piezometarske cjevčice (1) koje pokazuju veličinu statičkog pritiska mjerenog u pravcu okomito na smjer strujanja, kako bi se izbjegao utjecaj pritiska usljed kretanja tekućine. Pitotove cijevčice sa savijenim uronjenim krajevima u smjeru strujanja (2) po zakonu o spojenim posudama imaju istu razinu kao i posuda (3). Piezometarska i brzinska visina mogu se odrediti pomoću piezometarske i Pitotove cijevi. Zbir tih visina je konstantna i jednaka H, bez obzira koju strujnu cijev promatramo.

Na užim mjestima statički pritisak je manji, a na širim veći. U ravnomjernom strujanju tekućine kroz cijev brzina u užim dijelovima je veća, iz čega proizlazi da je na mjestima manje brzine strujanja statički pritisak veći, a na mjestima veće brzine manji.

Osnovne i izvedene mjerne jedinice koje se koriste u Bernoullijevoj jednačini

ρ – Gustoća - $(kg/m^{3})$

S - presjek predstavlja površinu poprečnog presjeka - $(m^{2})$.

p - statički pritisak - (Pa)

v - brzina - (m/s)

m – masa tekućine - (kg)

R - mehanički rad - (W)

V - volumen mase tekućine - $(m^{3})$

• Bernoullijeva jednačina koristi SI sistem jedinica.
  • $\ z$ geodetska visina, odnosno visina težišta poprečnog presjeka u odnosu na neku horizontalnu ravan u $\ (m)$
  • $\ p \over \rho g$ piezometarska ili visina pritiska, odnosno visina piezometarskog pritiska koju pokazuje visina stupca tekućine u piezometarskoj cijevi u $\ (m)$
  • $\ {v^{2} \over 2g}$ je brzinska visina u $\ (m)$, a brzina $\ v$ predstavlja brzinu koju bi tijelo imalo kada bi bilo u slobodnom padu.
  • Ukupan zbir energija daje Bernoullijevu jednačinu

Ulaskom u uži dio cijevi, presjeka $S_{2}$ i statičkog pritiska $p_{2}$, tekućina dobije veću brzinu $v_{2}$. Masa tekućine m ima u širem dijelu cijevi kinetičku energiju:

${\frac {m\cdot v_{1}^{2}}{2}}$

a kad uđe u uži dio:

${\frac {m\cdot v_{2}^{2}}{2}}$

Povećanje kinetičke energije posljedica je mehaničkog rada R koji je nastao zbog razlike pritisaka ($p_{1}-p_{2}$) $s_{1}$ pri kretanju mase m tekućine iz šireg dijela cijevi u uži na putu ΔS:

R = ($p_{1}-p_{2}$) $s_{1}$ ΔS

R= ($p_{1}-p_{2}$) V , gdje je V volumen mase tekućine.

Taj je rad jednak povećanju kinetičke energije:

($p_{1}-p_{2}$) V = ${\frac {m\cdot v_{2}^{2}}{2}}$ - ${\frac {m\cdot v_{1}^{2}}{2}}$

Dijeljenjem gornje jednakosti s volumenom, znajući da je gustoća ρ = ${\frac {m}{V}}$, dobijamo Bernoullijevu jednačinu:

$p_{1}$ + ${\frac {\rho \cdot v_{1}^{2}}{2}}$ = $p_{2}$ + ${\frac {\rho \cdot v_{2}^{2}}{2}}$ = $p_{3}$ + ${\frac {\rho \cdot v_{3}^{2}}{2}}$ = konst.

Izrazi ${\frac {\rho \cdot v_{1}^{2}}{2}}$ , $p_{2}$ + ${\frac {\rho \cdot v_{2}^{2}}{2}}$ i $p_{3}$ + ${\frac {\rho \cdot v_{3}^{2}}{2}}$ prikazuju pritisak koji je nastao usljed strujanja tekućine i zove se dinamički pritisak.

Oblik Bernoullijeve jednačine za idealnu tekućinu

Osnovne pretpostavke pod kojima vrijedi ova jednačina jesu:

1. tekućina je idealna - nestišljiva tekućina, linija energije je konstantna duž presjeka
2. Stacionarno strujanje

$\ z_{1}+{p_{1} \over \rho g}+{v_{1}^{2} \over 2g}=z_{2}+{p_{2} \over \rho g}+{v_{2}^{2} \over 2g}=H$

• • $\ H$ predstavlja hidrodinamički pritisak ili ukupnu specifičnu energiju u $\ (m)$.

Izvod Bernoullijeve jednačine preko zakona održanja količine kretanja

Bernoullijeva jednačina je prvi puta izvedena 1738. godine primjenom zakona održanja količine kretanja.

Osnovne pretpostavke pod kojima vrijedi ovaj izvod jesu:

1. fiktivna cijev ili proračun za konačni element neke cijevi,
2. Stacionarno strujanje ili postupno promjenjivo strujanje.

Izvod Bernoullijeve jednačine preko Eulerovog integrala

Eulerove diferencijalne jednačine kretanja tekućine - implicitni oblik

$\ {\frac {1}{\rho }}{\frac {\delta p}{\delta x}}=X-{\frac {du}{dt}}$ ... ... ...(1E)
$\ {\frac {1}{\rho }}{\frac {\delta p}{\delta y}}=Y-{\frac {dv}{dt}}$ ... ... ...(2E)
$\ {\frac {1}{\rho }}{\frac {\delta p}{\delta z}}=Z-{\frac {dW}{dt}}$ ... ... ...(3E)

$\ \rho =konst$ - nema općeg rješenja jer imamo 4 nepoznanice. Rješenje je moguće samo ako definiramo pretpostavku koja će eliminirati nepoznanicu viška.

Osnovna pretpostavka:

• imamo stacionarno strujanje

matematičke transformacije - (1E) množimo s dx, (2E) množimo s dy, (3E) množimo s dz i saberemo dobivene jednačine.

$\ {\frac {1}{\rho }}\left({\frac {\delta p}{\delta x}}dx+{\frac {\delta p}{\delta y}}dy+{\frac {\delta p}{\delta z}}dz\right)=Xdx+Ydy+Zdz-{\Bigg (}du\overbrace {\frac {dx}{dt}} ^{u}+dv\overbrace {\frac {dy}{dt}} ^{v}+dw\overbrace {\frac {dz}{dt}} ^{w}{\Bigg )}$,

pa dobijemo jednačinu:

$\ 0=Xdx+Ydy+Zdz-{\frac {1}{\rho }}\delta p-(udu+vdv+wdw)$

možemo derivirati

$\ udu={\frac {1}{2}}du^{2}$
$\ vdv={\frac {1}{2}}dv^{2}$
$\ wdw={\frac {1}{2}}dw^{2}$

Dakle, sada imamo ovaj oblik jednačine

$\ 0=Xdx+Ydy+Zdz-{\frac {\delta p}{\rho }}-{\frac {1}{2}}d(u^{2}+v^{2}+w^{2})$
$\ 0=Xdx+Ydy+Zdz-{\frac {\delta p}{\rho }}-{\frac {1}{2}}d(W^{2})$

• ako imamo strujnu cijev u kojoj djeluje samo gravitacija u normalnom koordinatnom sistemu. Možemo pojednostavniti ovako:

$\ X=0,Y=0,Z=-g$
$\ -gdz-{\frac {\delta p}{\rho }}-{\frac {1}{2}}d(W^{2})=0...operacije/\int /:-g$
I konačno Eulerov integral koji predstavlja izvod Bernoullijeve jednačine:
$\ z+{\frac {p}{\rho g}}+{\frac {W^{2}}{2g}}=konstanta$

Oblik Bernoullijeve jednačine za realnu tekućinu

$\ z_{1}+{p_{1} \over \rho g}+{\alpha _{1}v_{1}^{2} \over 2g}=z_{2}+{p_{2} \over \rho g}+{\alpha _{2}v_{2}^{2} \over 2g}+\Delta H$

• • $\ \Delta H$ je dio specifične energije utrošen na svladavanje hidrodinamičkih otpora strujanju kapljevine. Izražava se u $\ (m)$.

Coriolisov koeficijent

Naziva se i koeficijent kinetičke energije $\ \alpha _{1,2}$. On pokazuje odnos stvarne kinetičke energije mase fluida koji protječe poprečnim presjekom u jedinici vremena i kinetičke energije određene iz uvjeta da su brzine u svim tačkama presjeka jednake (srednja brzina). Koeficijent kinetičke energije je bezdimenzionalna jedinica.

Koeficijent kinetičke energije najčešće ima sljedeće vrijednosti:

• • kod strujanja u cijevima $\alpha =1,0$
  • kod strujanja u otvorenim vodotocima $\alpha =1,1$
  • vrijednost $\alpha$ možemo računati ovom formulom:

$\ \alpha ={\frac {\int _{A}v^{3}dA}{v_{sr}^{3}A}}$ - postavlja se uslov da je $\alpha \geq 1$

Praktična primjena Bernoullieve jednačine

Primjer cijevi pod pritiskom

Cijev pod pritiskom

Znamo: $\ d=konstantno,Q=konstantno\quad \rightarrow \quad v=konstantno$.

gubitak pritiska predstavlja razliku piezometarskih visina u presjecima (1) i (2). Za slučaj da je cijev horizontalna vrijedi: $z_{1}=z_{2}$

$\ z_{1}+{\frac {p_{1}}{\rho g}}=z_{2}+{\frac {p_{2}}{\rho g}}+\Delta H$
$\ \Delta H=\left(z_{1}+{\frac {p_{1}}{\rho g}}\right)-\left(z_{2}+{\frac {p_{2}}{\rho g}}\right)$

Zaključak

$\ p_{s}+\ p_{d}=p_{u}=konst.$

gdje je $\ p_{s}$ statički pritisak, $\ p_{d}={\frac {\rho \cdot v^{2}}{2}}$ dinamički pritisak, a $\ p_{u}$ ukupni pritisak, konstantan u cijelom horizontalnom cjevovodu bez obzira na presjek.

• Bernoullijev zakon ili Bernoullijeva jednačina služi za proračun brzine, pritiska ili gubitaka kod protoka tekućine kroz otvorene i zatvorene vodotoke za idealnu i realnu tekućinu. Pošto se radi o tekućinama, tj. fluidima, ova jednačina služi kao temeljna postavka za objašnjavanje uzgona aeroprofila.

Također pogledajte

• Navier–Stokesove jednačine
• Hidraulika