Stehiometrija

Stehiometrija je stanje i način izračunavanja relativne količine reagensa i proizvoda u hemijskim reakcijama.

Reakcija sagorijevanja metana.

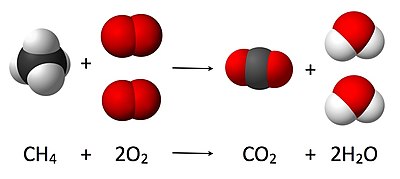
Stehiometrija je utemeljena na zakonu održanja mase, gdje je ukupna masa reagenasa jednaka ukupnoj masi proizvoda. To znači da se odnosi između količine reagenasa i proizvoda obično ponašaju kao odnosi pozitivnih cijelih brojeva. To istovremeno govori da ako su poznati iznosi odvojenih reagenasa, onda se može izračunati i iznos proizvoda. Saglasno tome, ako je poznata količina jednog reagensa i količina proizvoda, empirijski se može odrediti jedan od reagenasa, a zatim se može izračunati i iznos drugih reagenasa.

Ovi odnosi se mogu prikazati uravnoteženom jednačinom:

CH₄ + 2 O₂ → CO₂ + 2 H₂O.

Ovdje jedna molekula metana reagira sa dvije molekule plinovitog kisika, pa nastaju jedna molekula ugljik-dioksida i dvije molekule vode. Stehiometrija mjeri ove količinske odnose, a koristi se za određivanje količine proizvoda/reagenasa koji su proizvodeni/potrebni u datoj reakciji. Opisani količinski odnosi među supstancama u hemijskoj reakciji poznati su kao reakcijska stehiometrija. U gornjem primjeru, reakcijska stehiometrija mjeri odnos između metana i kisika koji u međusobnoj reakciji stvaraju ugljik-dioksid i vodu.

Zbog poznatog odnosa molske i atomske težine, dobijeni stehiometrijski koeficijenti mogu se koristiti za određivanje težine u reakciji koja je opisana u uravnoteženoj jednačini. To se zove kompozicijska stehiometrija.

Plinska stehiometrija bavi se reakcijama koje uključuju plinove, a na osnovu poznate temperature, pritiska i zapremine može se pretpostaviti da li je dati uzorak idealan plin. Za plinove, odnos volumena je idealno isti kao i onaj po zakonu o idealnom plinu, ali se odnos mase jedne reakcije mora izračunati iz molekulskih masa reagenasa i proizvoda. U praksi, zbog postojanja izotopa, koriste se molarne mase, umjesto da se izračunava odnos masa.

Etimologija

Izraz stehiometrija je prvi put koristio Jeremias Benjamin Richter 1792. godine, kada je objavljen prvi tom njegove knjige pod nazivom Stehiometrija ili umjetnost mjerenja hemijskih elemenata (Stoichiometry or the Art of Measuring the Chemical Elements). Naziv je izveden iz grčkih riječi στοιχεῖον - stoicheion = element + μέτρον – metron = mjera. U patrističkom grčkom, riječ stoichiometria je koristio patrijarh Nikefor I Carigradski kada se odnosio na broj linijskih tačaka kanonskog Novog zavjeta i nekih od Apokrifa.

Definicija

Stehiometrijska količina ili stehiometrijske odnos reagenasa je njihova najpovoljnija količina ili odnos, a pod pretpostavkom da je reakcija kompletna, potebno je znati da:

1. svi reagensi se troše;
2. nema nedostatka reagenasa;
3. ne postoji višak reagensa.

Stehiometrija počiva na osnovnim zakonima koji pomažu bolje razumijevanje odnosa u reakcijama kao što su: zakon održanja mase, zakon određenih proporcija (odnosno, zakon stalnog sastava), zakon više proporcija i zakon recipročnih proporcija. U principu, u hemijskim reakcijama se sjedinjuju određeni omjeri hemikalija. Hemijske reakcije ne mogu ni stvoriti ni uništiti tvar, niti transmutirati jedan hemijski element u drugi, a iznos svakog elementa mora biti isti u cijelokupnoj reakciji. Naprimjer, broj atoma određenog elementa X na reaktantskoj strani mora biti jednak broju atoma tog elementa na strani proizvoda, bez obzira da li su ili ne svi od tih atoma zapravo uključeni u reakciju.

Hemijske reakcije, kao makroskopske jedinice operacija, sastoje se od veoma velikiog broja elementarnih reakcija, gdje jedna molekula reaguje s drugom molekulom. Kada molekula (ili njena polovina) reaguje, nastaje završni skup atoma u proizvodu, a odnos između reagenasa u potpunoj reakciji je u integriranom odnosu. Reakcija može trošiti više od jedne molekule, a stehiometrijski broj se objašnjava kao pozitivan broj za proizvode (zbirno) i negativan za potrošene reagense.

Različiti elementi imaju različite atomske mase, a kao zbirovi pojedinačnih atoma, molekule imaju određenu molarnu masu, koja je mjerena jedinicom mola (6,02   ×  10²³ pojedinačne molekule, a naziva se Avogadrova konstanta). Po definiciji, ugljik-12 ima molarnu masu od 12 g/mol. Tako se izračunava stehiometrija mase, gdje je broj molekula potrebnih za svaki reagens izražen u molovima i pomnožen sa molarnom masom svakog reagensa po molu reakcije. Odnosi masa mogu se izračunati dijeljenjem svakog od njih i ukupnom masom cijele reakcije. Elementi u svom prirodnom stanju su smjese izotopa s različitom masom, čime se pokazuje da atomske mase, a time i molarne mase nisu baš cijeli brojevi. Naprimjer, umjesto tačne proporcije 14:3, dobije se 17,04   kg amonijaka 14,01   kg dušika i 3  ×  1,01   kg vodika, jer prirodni dušik sadrži male količine dušika-15 , a prirodni vodik sadrži vodik-2 (deuterij).

Stehiometrijski reagens je onaj reagens koji se troši u reakciji, za razliku od katalitskog reagensa, koji se u ukupnoj reakciji ne troši, jer reaguje u jednom koraku, a zatim se i obnavlja u još jednom.

Pretvaranje grama u molove

Stehiometrija se ne koristi samo za uravnotežavanje hemijske jednačine, nego i u pretvaranju grama supstsance u molove ili grama u mililitre. Naprimjer, da bi se pronašao iznos NaCl (natrij hlorida) u 2,00 g supstance, treba učiniti slijedeće:

${\frac {2,00{\mbox{ g NaCl}}}{58,44{\mbox{ g NaCl mol}}^{-1}}}=0,034\ {\text{mol}}$

U gornjem primjeru, kada je napisan u djelimičnom obliku, grami čine umnožavajući pojam, koji je jednak veličini 1 (g/g   =  1) sa rezultirajućim iznosom u molovima (jedinici koja je potrebna), kao što je prikazano u sljedećoj jednačini:

$\left({\frac {2,00{\mbox{ g NaCl}}}{1}}\right)\left({\frac {1{\mbox{ mol NaCl}}}{58,44{\mbox{ g NaCl}}}}\right)=0,034\ {\text{mol}}$

Molarna proporcija

Stehiometrija se često koristi za uravnotežavanje hemijske jednačine (stehiometrijska reakcija). Naprimjer, dvije diatomske molekule plina, vodika i kisika, mogu se sjediniti pri čemu se dobije tečna voda, u egzotermnoj reakciji, a prema slijedećoj jednačini:

2 H₂ + O₂ → 2 H₂O

Stehiometrijska reakcija u gornjoj jednačini opisuje da je omjer vodika, kisika i molekule vode 2:1:2.

Molarni odnos omogućava pretvaranje između molova jedne supstance u molove drugog. Naprimjer, u reakciji:

2 CH₃OH + 3 O₂ → 2 CO₂ + 4 H₂O

Količina vode koja se proizvodi potrošnjom 0,27 mola CH₃OH, dobija se primjenom molskog odnosa između CH₃OH i H₂O od 2 do 4.

$\left({\frac {0,27{\mbox{ mol }}\mathrm {CH_{3}OH} }{1}}\right)\left({\frac {4{\mbox{ mol }}\mathrm {H_{2}O} }{2{\mbox{ mol }}\mathrm {CH_{3}OH} }}\right)=0,54\ {\text{mol }}\mathrm {H_{2}O}$

Naziv stehiometrija se također često koristi za molarne proporcije elemenata u stehiometrijskom jedinjenju (kompozicijska stehiometrija). Naprimjer, stehiometrija vodika i kisika u H₂O je 2:1. U stehiometrijskom jedinjenju, molarne proporcije su cijeli brojevi.

Određivanje iznosa proizvoda

Stehiometrija se također može upotrijebiti za pronalaženje količine proizvoda reakcija. Ako se komad čvrstog bakra (Cu) doda u vodeni rastvor srebro-nitrata (AgNO₃), u reakciji jednostrukog premještanje, stvaraju se vodeni bakar(II)-nitrat (Cu(NO₃)₂) i čvrsto srebro (Ag). Koliko se dobije srebra, ako se 16,00 grama Cu doda u rastvor, za pojavu viška srebrenog nitrata? U traženju odgovora se primjenjuju slijedeći koraci:

1. Napisati i uravnotežiti jednačinu;
2. Izraziti masu u molima: pretvaranjem grama Cu u molove Cu;
3. Naći molni odnos: pretvaranjem molova Cu u molove proizvedenog Ag;
4. Odrediti molove u masi: pretvaranjem molova Ag u grame proizvedenog Ag.

Potpuno uravnotežena jednačina je:

Cu + 2 AgNO₃ → Cu(NO₃)₂ + 2 Ag

U koraku masa -mol, masa bakra (16,00 g) se pretvara u molove bakra dijeljenjem mase bakra njegovom molekulskom masom: 63,55 g/mol.

$\left({\frac {16,00{\mbox{ g Cu}}}{1}}\right)\left({\frac {1{\mbox{ mol Cu}}}{63,55{\mbox{ g Cu}}}}\right)=0,2518\ {\text{mol Cu}}$

Zatim se, preko iznosa Cu u molovima (0,2518), traži molski odnos. To se izražava kao koeficijent u balansiranoj reakciji: Cu i Ag su u odnosu 1:2.

$\left({\frac {0,2518{\mbox{ mol Cu}}}{1}}\right)\left({\frac {2{\mbox{ mol Ag}}}{1{\mbox{ mol Cu}}}}\right)=0,5036\ {\text{mol Ag}}$

Sada, kada je poznata količina proizvedenog Ag = 0,5036 mol, ovaj iznos se pretvara u grame proizvedenog Ag i dolazi se do konačnog odgovora:

$\left({\frac {0,5036{\mbox{ mol Ag}}}{1}}\right)\left({\frac {107,87{\mbox{ g Ag}}}{1{\mbox{ mol Ag}}}}\right)=54,32\ {\text{g Ag}}$

Ovaj skup proračuna može se dalje sažeti u jednostruki korak:

$m_{\mathrm {Ag} }=\left({\frac {16,00{\mbox{ g }}\mathrm {Cu} }{1}}\right)\left({\frac {1{\mbox{ mol }}\mathrm {Cu} }{63,55{\mbox{ g }}\mathrm {Cu} }}\right)\left({\frac {2{\mbox{ mol }}\mathrm {Ag} }{1{\mbox{ mol }}\mathrm {Cu} }}\right)\left({\frac {107,87{\mbox{ g }}\mathrm {Ag} }{1{\mbox{ mol Ag}}}}\right)=54,32{\mbox{ g}}$

Ostali primjeri

Z propansku (C₃H₈) reakciju sa plinovitim kisikom (O₂), uravnotežena hemijska jednačina je:

C₃H₈ + 5 O₂ → 3 CO₂ + 4 H₂O

Masa vode se dobije ako 120 g propana (C₃H₈) izgori u višku kisika, tj. tada:

$m_{\mathrm {H_{2}O} }=\left({\frac {120,0{\mbox{ g }}\mathrm {C_{3}H_{8}} }{1}}\right)\left({\frac {1{\mbox{ mol }}\mathrm {C_{3}H_{8}} }{44,09{\mbox{ g }}\mathrm {C_{3}H_{8}} }}\right)\left({\frac {4{\mbox{ mol }}\mathrm {H_{2}O} }{1{\mbox{ mol }}\mathrm {C_{3}H_{8}} }}\right)\left({\frac {18,02{\mbox{ g }}\mathrm {H_{2}O} }{1{\mbox{ mol }}\mathrm {H_{2}O} }}\right)=196{\mbox{ g}}$.

Stehiometrijski omjer

Stehiometrija se koristi i za pronalaženje pravog iznosu jednog reagensa da "potpuno" reaguje s drugim reagensom u hemijskoj reakciji, tj. stehiometrijske količine ćiji ostaci reagenasa će se potrošiti kada se reakcija odvije. Jedan primjer je prikazan ispod, koristeći reakciju stvaranja legure željezo – aluminij:

Fe₂O₃ + 2 Al → Al₂O₃ + 2 Fe

Ova jednačina pokazuje da će 1 mol željezo(III)-oksida i 2 mola aluminija proizvesti 1 mol aluminij-oksida i 2 mola željeza. Tako, za kompletnu reakciju 85,0 g željezo(III)-oksida (0,532 mol), potrebno 28,7 g (1,06 mol) aluminija.

$m_{\mathrm {Al} }=\left({\frac {85,0{\mbox{ g }}\mathrm {Fe_{2}O_{3}} }{1}}\right)\left({\frac {1{\mbox{ mol }}\mathrm {Fe_{2}O_{3}} }{159,7{\mbox{ g }}\mathrm {Fe_{2}O_{3}} }}\right)\left({\frac {2{\mbox{ mol Al}}}{1{\mbox{ mol }}\mathrm {Fe_{2}O_{3}} }}\right)\left({\frac {26,98{\mbox{ g Al}}}{1{\mbox{ mol Al}}}}\right)=28,7{\mbox{ g}}$.

Ograničavajući reagens i postotak prinosa

Ograničavajući reagens je onaj reagens koji ograničava količinu proizvoda koji može nastati, ako se dati reagens potpuno potroši, što postaje prepreka nastavku reakcije. Višak reagens je onaj koji je preostao nakon što je reakcija zaustavljena zbog ograničenja iscrpljenog reagensa.

Pretpostavimo jednačinu prženja olovo-(II) sulfida (PBS) u kisiku (O₂) za proizvodnju olovo(II)-oksida (PbO) i sumpor-dioksida (SO₂):

2 PbS + 3 O₂ → 2 PbO + 2 SO₂.

Za određivanje teorijskog prinosa olovo(II) oksida, ako se 200,0 g olovo(II) sulfida i 200,0 g kisika zagrijava u otvorenom spremniku služi obrazac:

$m_{\mathrm {PbO} }=\left({\frac {200,0{\mbox{ g }}\mathrm {PbS} }{1}}\right)\left({\frac {1{\mbox{ mol }}\mathrm {PbS} }{239,27{\mbox{ g }}\mathrm {PbS} }}\right)\left({\frac {2{\mbox{ mol }}\mathrm {PbO} }{2{\mbox{ mol }}\mathrm {PbS} }}\right)\left({\frac {223,2{\mbox{ g }}\mathrm {PbO} }{1{\mbox{ mol }}\mathrm {PbO} }}\right)=186,6{\mbox{ g}}$

$m_{\mathrm {PbO} }=\left({\frac {200,0{\mbox{ g }}\mathrm {O_{2}} }{1}}\right)\left({\frac {1{\mbox{ mol }}\mathrm {O_{2}} }{32,00{\mbox{ g }}\mathrm {O_{2}} }}\right)\left({\frac {2{\mbox{ mol }}\mathrm {PbO} }{3{\mbox{ mol }}\mathrm {O_{2}} }}\right)\left({\frac {223,2{\mbox{ g }}\mathrm {PbO} }{1{\mbox{ mol }}\mathrm {PbO} }}\right)=930,0{\mbox{ g}}$.

Zato što se proizvode manji iznosi PbO za 200,0 g PbS, jasno je da je PbS ograničavajući reagens. U stvarnosti, dati prinos nije isti kao onaj koji je izračunat stehiometrijski, a postotak se tada izražava sljedećom jednačinom:

${\mbox{Postotak prinosa}}={\frac {\mbox{Dobijeni prinos}}{\mbox{Teorijski prinos}}}$

Ako se dobije 170,0 g olovo(II) oksida, postotak prinosa se izračunava na sljedeći način:

${\mbox{Postotak prinosa}}={\frac {\mbox{170,0 g PbO}}{\mbox{186,6 g PbO}}}=91,12\%$

Različite stehiometrije u konkurencijskim reakcijama

Od polaznog materijala, često je moguće dobiti više od jedne reakcije. Reakcije se mogu razlikovati u svojoj stehiometriji. Naprimjer, metilacija benzena (C₆H₆), putem Friedel–Craftove reakcije, a upotrebom AlCl₃ kao katalizatora, može nastati jednostruko metilizirani (C₆H₅CH₃), dvostruko metilizirani (C₆H₄(CH₃)₂ ili visoko metilizirani (C₆H_6−n(CH₃)_n) proizvodi, kako je prikazano u slijedećem primjeru:

C₆H₆ + CH₃Cl → C₆H₅CH₃ + HCl

C₆H₆ + 2 CH₃Cl → C₆H₄(CH₃)₂ + 2 HCl

C₆H₆ + n CH₃Cl → C₆H_6−n(CH₃)_n + n HCl

U ovom primjeru, reakcija se odvija pod kontrolom u dijelu relativnih koncentracija reagenasa.

Stehiometrijski koeficijent

U laičkom smislu, stehiometrijski koeficijent (ili stehiometrijski broj u IUPAC nomenklaturi) bilo koje komponente je broj molekula koje sudjeluju u reakciji kako je napisano.

Naprimjer, u reakciji CH₄ + 2 O₂ → CO₂ + 2 H₂O}}, stehiometrijski koeficijent CH₄ je -1, a stehiometrijske koeficijent O₂ je -2, za CO₂ bilo bi +1 i za H₂O to je +2.

Tehnički preciznije rečeno, stehiometrijski koeficijent u hemijskoj reakciji sistema i-te komponente se objašnjava kako slijedi. Naprimjer, u reakciji CH₄ + 2 O₂ → CO₂ + 2 H₂O, stehiometrijski koeficijent CH₄ je −1, a za O₂ je −2, za CO₂ bit će +1 i za H₂O je +2:$\nu _{i}={\frac {\Delta N_{i}}{\Delta \xi }}\,$ ili

$\Delta N_{i}=\nu _{i}\Delta \xi \,$,

gdje

• N_i = broj molekula i, a
• ξ = progres varijable ili proširenje reakcije.

Stehiometrijski matriks

U složenim reakcijama, stehiometrija je često predstavljena u mnogo kompaktnijem obliku zvanom stehiometrijski matriks ili matrica, koji se označava simbolom N.

Ako reakcijska mreža ima n pojdinačnih reakcija i m uključenih vrsta molekula, tada stehiometrijski matriks može imati odgovarajući m redova i n kolona.

Naprimjer, podrazumijevajući donji sistem prikazanih reakcija, slijedi:

S₁ → S₂

5 S₃ + S₂ → 4 S₃ + 2 S₂

S₃ → S₄

S₄ → S₅

Ovaj sistem se sastoji od četiri reakcije i pet različitih vrsta molekula. Stehiometrijska matrica za ovaj sistem se može pisati kao: $\mathbf {N} ={\begin{bmatrix}-1&0&0&0\\1&1&0&0\\0&-1&-1&0\\0&0&1&-1\\0&0&0&1\\\end{bmatrix}}$,

gdje redovi odgovaraju S₁, S₂, S₃, S₄, odnosno S₅. Proces pretvaranja reakcijske sheme u stehiometrijski matriks može biti sa gubicima transformacija. Naprimjer, stehiometrija u drugoj reakciji se može pojednostaviti kada je uključena u matricu. To znači da nije uvijek moguć oporavak prvobitne reakcijske sheme iz stehiometrijske matrice. Stehiometrijski matriks je često kombiniran sa stopom vektora v i vektorom vrste molekula S, a za stvaranje kompaktne jednačine, koja opisuje stopu promjena molekulskih vrsta:

${\frac {d\mathbf {S} }{dt}}=\mathbf {N} \cdot \mathbf {v} .$

Stehiometrija plinova

Plinska stehiometrija je količinski odnos između reagenasa i proizvoda u hemijskim reakcijama onih reagenasa koji proizvode plinove. Plinska stehiometrija se primjenjuje kada se proizvedeni plinovi nakupe toliko da postanu idealni, a temperatura, pritisak i zapremina sasvim poznati. U ovim proračunima se primjenjuje zakon idealnog plina. Često, ali ne uvijek, u stehiometrijskim proračunima se standardna temperatura i pritisak (STP) uzimaju kao 0 °C i 1 bar.

Proračuni plinske stehiometrije se primjenjuju i za nepoznatu zapreminu ili masu plinovitih proizvoda ili reagenasa. Naprimjer, ako se želi izračunati zapremina plinovitih NO₂ proizvoda sagorijevanja, putem reakcije:

4 NH₃(g) + 7 O₂(g) → 4 NO₂(g) + 6 H₂O(l),

mogu se izvesti slijedeći proračuni:

$100\,\mathrm {g\,NH_{3}} \cdot {\frac {1\,\mathrm {mol\,NH_{3}} }{17,034\,\mathrm {g\,NH_{3}} }}=5,871\,\mathrm {mol\,NH_{3}}$.

U gornjoj reakciji sagorijevanja molarni odnos NH₃ prema NO₂ je 1:1, uz nastanak 5,871 mola NO₂. Tada se za određivanje zapremine može primijeniti zakon idealnog plina na 0 °C (273,15 K) i pritisku od 1 atmosfere, upotrebom donje plinske konstante R = 0,08206 L·atm·K⁻¹·mol⁻¹ :

${\begin{aligned}PV&=nRT\\V&={\frac {nRT}{P}}\\&={\frac {5,871\cdot 0,08206\cdot 273,15}{1}}\\&=131,597\,\mathrm {L\,NO_{2}} \end{aligned}}$.

Plinska stehiometrija često uključuje poznavanje molske mase plina date gustine. Da bi se dobili odnosi između gustine i molarne mase idealnog plina, preuređuje se obrazac idealnog plina:

$\rho ={\frac {m}{V}}$    i    $n={\frac {m}{M}}$

i tako:

$\rho ={\frac {MP}{R\,T}}$,

gdje:

• P = apsolutni pinski pritisak;
• V = zapremina plina
• n = iznos (u molovima);
• R = univerzalna konstanta idealnog plina;
• T = apsolutna temperatura plina;
• ρ = gustina plina na T i P;
• m = masa plina;
• M = molska masa plina.

Uobičajeni stehiometrijski odnos zrak-gorivo

U reakciji sagorijevanja, kisik reaguje s gorivom, a tačka na kojoj se troši baš sav kisik i svo gorivo se definira kao stehiometrijska tačka. Sa više kisika (nadstehiometrijsko sagorijevanje), nešto od toga ostaje neodreagirano. Isto tako, ako je sagorijevanje nepotpuno, zbog nedostatka kisika, gorivo i dalje ostaje van reakcije. (Nereaktivno gorivo može ostati zbog sporog sagorijevanja ili nedovoljnog miješanje goriva i kisika – što nije zbog stehiometrije). Različita ugljikovodikova goriva imaju različite sadržaje ugljika, vodika i drugih elemenata, zbog čega je i njihova stehiometrija promjenljiva, kako slijedi.

Gorivo	Odnos mase	Odnos zapremine	Postotak mase goriva
Benzin	14,7 : 1	—	6,8%
Prirodni plin	17,2 : 1	9,7  : 1	5,8%
Propan (LP)	15,67 : 1	23,9 : 1	6,45%
Etanol	9 : 1	—	11,1%
Metanol	6,47 : 1	—	15,6%
n-Butanol	11,2 : 1	—	8,2%
Vodik	34,3 : 1	2,39 : 1	2,9%
Dizel	14,5 : 1	—	6,8%
Metan	17,19 : 1	9,52 : 1	5,5%

Benzinski motori mogu raditi sa stehiometrijskim odnosom zrak-gorivo, jer benzin je vrlo nestabilan i lahko se miješa (prskanjem sa sprejom ili karburacijom) sa zrakom, prije paljenja. Dizelski motori, za razliku od toga, rade sporije i s više dostupnog zraka od zahtjeva jednostavnih stehiometrija. Dizel gorivo je manje nestabilno i uspješno sagorijeva jer se ubrizgava, ostavljajući manje vremena za isparavanje i miješanje. Zato se u stehiometrijskom odnosu stvara čađ (crni dim).

Također pogledajte

• Geometrija molekule

Vanjski linkovi

• Engine Combustion primer from the University of Plymouth
• Free Stoichiometry Tutorials from Carnegie Mellon's ChemCollective
• Stoichiometry Add-In for Microsoft Excel Arhivirano 11. 5. 2011. na Wayback Machine for calculation of molecular weights, reaction coëfficients and stoichiometry.
• Reaction Stoichiometry Calculator a comprehensive free online reaction stoichiometry calculator.
• Stoichiometry Calculator a unit conversion calculator for individual compound stoichiometry.