Pravougaonik

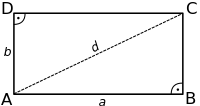
Pravougaonik je četverougao, koji pripada paralelogramima. Ima četiri prava ugla. Naspramne stranice su uvijek jednake dužine, kao i dijagonale.

Pravougaonik

Definicija

Paralelogram čiji su svi uglovi jednaki zove se pravougaonik.

Teorema

1. Pravougaonik ima dvije ose simetrije koje prolaze kroz njihov centar simetrije paralelne su njegovim stranicama i međusobno normalne.
2. Dijagonale pravougaonika su jednake. Njihov presjek je centar opisane kružnice.

Ako su mu sve stranice jednake dužine, onda je riječ o kvadratu. Dužina dužih stranica se definiše kao dužina cijelog pravougaonika, a dužina kraćih kao širina pravougaonika.

Četverougao je pravougaonik ako je ispunjen jedan od uslova

1. svi uglovi su jednaki
2. četverougao sa svim pravim uglovima
3. paralelogran sa najmanje jednim pravim uglom
4. četverougao kod koga su trouglovi $ABD$ i $DAC$ podudarni
5. konveksni četverougao sa uzastopnim stranicama $a,\ b,\ c,\ d$ čija je površina ${\tfrac {1}{4}}(A+C)(b+d)$
6. konveksni četverougao sa uzastopnim stranicama $a,\ b,\ c,\ d$ čija je površina s ${\tfrac {1}{2}}{\sqrt {(a^{2}+c^{2})(b^{2}+d^{2})}}$.

Formule

Površina pravougaonika iznosi $P=a\cdot \;b$

Obim $O=2(a+b)$

Poluobim pravougaonika $s=a+b$

Dijagonala $d={\sqrt {a^{2}+b^{2}}}$

r (radijus opisane kružnice): $r={\frac {d}{2}}$

Uglovi između stranica i dijagonala $\varphi =arctg(b/a)$ i $\varphi _{2}=arctg(a/b)$

uglovi između dijagonala $\phi _{1}=\pi -2\varphi _{1}$ i $\phi _{2}=\pi -2\varphi _{2}$

$\phi _{1}+\phi _{2}=\pi$

Dijagonala pravougaonika

Dijagonala pravougaonika je duž koja spaja dva njegova tjemena koja nemaju ni jednu zajedničku stranicu. Pravougaonik ima tačno dvije dijagonale, i one su jednakih dužina.

$d={\sqrt {a^{2}+b^{2}}}$

Osobine pravougaonika

1. pravougaonik je paralelogram
2. naspramne stranice pravougaonika su jednake,
3. svi uglovi pravougaonika su jednaki,
4. dijagonale pravougaonika su jednake i polove se,
5. centar opisane kružnice se nalazi u presjeku dijagonala,
6. poluprečnik kružnice opisane oko pravougaonika je jednak polovini dijagonale pravougaonika,
7. u pravougaonik se ne može upisati kružnica.

Posebni pravougaonici

Zlatni pravougaonik

Pravougaonik čije dužine stranica ispunjavaju uslov $\textstyle {\frac {a}{b}}\,=\,{\frac {b}{a-b}}$ je zlatni pravougaonik

Savršeni pravougaonik

Četverougao je savršen ako ga možemo prekriti kvadratima različite površine. Takav je pravougaonik (32 × 33). Može se podijeliti na 9 kvadrata čije stranice imaju dužinu $1,\ 4,\ 7,\ 8,\ 9$, $10,\ 14,\ 15\ i\ 18$

Izvori

1. http://www.boske.rs/stranice/povrsine_geometrijskih_figura.html
2. http://formule.pismenizadaci.com/cetvorougao.html
3. http://formule.pismenizadaci.com/pitagorina_teorema.html
4. Rectangle
5. Rectangle
6. Area of a rectangle