Molekulska orbitala
Molekulska orbitala (skr. MO) – u hemiji – je matematička funkcija koja opisuje ponašanje elektrona kao talasa u molekuli. Ova funkcija se može primijeniti za izračunavanje fizičkih i hemijskih osobina, kao što je nalaženje elektrona u određenom dijelu prostora. Molekulske orbitale se najčešće konstruiraju kombinacijom atomskih ili hibridnih orbitala svakog od atoma u datoj molekuli.[1][2][3]
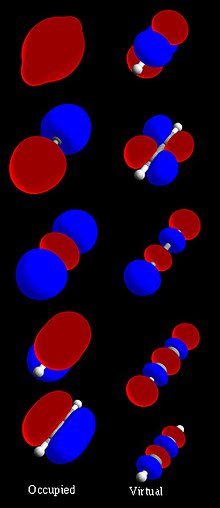
Pregled
urediMolekulska orbitala može poslužiti za određivanje elektronske konfiguracije molekula: prostorne distribucije i energije jednog ili para elektrona. Molekulske orbitale se obično prikazuju kao linearna kombinacija atomskih orbitala, osobito u kvalitativnim ili aproksimativnim analizama. Ovaj metod je nezamjenljiv za ostvarivanju jednostavnog modela veza u molekuli, kao u primjeru teorijom molekulskih orbitala. Molekulska orbitala opisuje ponašanje jednog elektrona u električnom polju koje stvaraju jezgro i prosječna raspodjela drugih elektrona. Ako se u orbitali nalaze dva elektrona, Paulijev princip isključenja nalaže da moraju imati suprotan spin. Molekulska orbitala predstavlja približan opis talasne funkcije elektrona u molekuli, a koji su visoko tačni nemaju orbitale.[4][5]
Kvalitativni opis
urediSve talasno mehaničke, odnosno talasno-mehaničke zakonitosti koje važe za atom, važe i za složeniji sistem: molekulu. To znači da su, prema ovoj teoriji i metodu, elektroni u molekuli raspoređeni po odgovarajućim orbitalama, kao i u atomu. Osnovna razlika je u tome da su atomske orbitale monocentrične, a molekulske policentrične, tj. izgrađene oko dva ili više atomskih jezgara. Molekulske orbitale se mogu ostvariti linearne kombinacije atomskih orbitala. Kao rezultat kombinacije dvije atomske orbitale, dobijaju se dvije molekulske orbitale predstavljene zbirom odnosno razlikom atomskih orbitala.
Broj molekulskih orbitala je jednak broju atomskih orbitala koje su uključene u linearnu kombinaciju.
Primjeri
urediH2
urediStvarni dio valne funkcije je plava kriva, a imaginarni dio – crvena.
Crvena tačkasta linija je lokacija jezgara. Valna funkcija elektrona oscilira suglasno Schrödingerovoj valnoj jednadžbi, a orbitale su njene stojeći valovi.
Frekvencije stojećih valova je proporcijska kinetičkoj enersgiji orbitala
(Ovaj prikaz je jednodimenzionalni isječak trodimenzionalnog sistema.)
Molekula vodika se sastoji od dva atoma vodonika koje označavamo sa H' i H". Linearnom kombinacijom 1s' i 1s" atomskih orbitala dobiju se dvije molekulske orbitale: jedna vezivna i druga antivezivna. Preva se dobija zbrajanjem atomskih orbitala i odgovara stanju sistema u kojem je elektron u vezivnoj oblasti. Antivezivna molekulska orbitala se odnosi na oduzimanje atomskih orbitala, a odgovara stanju sistema u kojem se elektron nalazi u antivezivnoj oblasti. Energija vezivnih orbitala je niža od atomskih orbitala, dok antivezivne orbitale imaju veću energiju. Sklapanje molekula od atoma se opisuje kao preraspoređivanje elektronskih u molekulske orbitale. U molekuli vodika su dva elektrona, pri čemu se oba raspoređuju u vezivnu orbitalu, pri čemu sistem postaje energetski slabiji. Pritom se stvara kovalentna veza.
Red veze se definira kao broj elektrona u vezivnim orbitalama umanjen za broj elektrona u antivezivnim orbitalama, pa sve podijeljeno sa dva. U primjeru molekula vodika postoje dva elektrona u vezivnoj orbitali, a nema ih u antivezivnim orbitalama, pa je red veze jedan, uz jednu vezu između atoma vodika.
He2
urediUosnovnom stanju, helij u 1s orbitali ima dva elektrona. U hipotetskom primjeru molekula He2, dva elektrona bi popunila vezivnu orbitalu, a dva antivezivnu, pri čemu nastala elektronska gustina ne podržava formiranje veze između atoma i molekula. Tada je red veze nula jer ona ne postoji. Da bi uspostava hemijske veze bila moguća, tj. da se kreira molekula jedinjenja, potrebno je da broj elektrona u vezivnim orbitalama bude veći nego u antivezivnim. Molekula HeH bi imala malo manju energiju nego početni atomi, ali veću energetsku prednost, odnosno H2 + 2 He ima manju energiju, tako da molekul HeH opstaje samo kratko.
Energetski dijagrami
urediU slučaju složenijih molekula, talasno mehanički model je pogodan za kvantitivni opis veza, ali ne i za kvalitativni. Zato se uvode energetski dijagrami, u kojima se molekulske orbitale predstavljaju horizontalnim linijama, pri čemu su orbitale koje imaju višu energiju jače naznačene. Degenerirane orbitale (orbitale sa istom energijom) su predstavljene na istoj razini, ali se između njih nalazi razmak. Elektroni se popunjavaju jedan po jedan, pridržavajući se Paulijevog principa isključenja i Hundovog pravila tj. u jednoj orbitali se nalaze maksimalno dva elektrona suprotnog spina, a na istom energetskoj razini elektroni se popunjavaju tako da ima maksimalan broj nesparenih elektrona, pa se zatim uparuju.
HOMO i LUMO orbitale
urediNajviša od popunjenih molekulskih orbitala se naziva HOMO, a najniža nepopunjena je LUMO. Razlika između energija HOMO i LUMO molekulskih orbitala se naziva zabranjena zona koja može poslužiti kao mjera za sposobnost pobuđivanja molekula: što je energija manja – molekulu je lakše pobuditi.
Također pogledajte
urediReference
uredi- ^ Petrucci R.H., Harwood W.S. and Herring F.G. (2002): General Chemistry, 8th Ed. Prentice-Hall, New York, ISBN 0-13-014329-4.
- ^ Laidler K. J. (1978): Physical chemistry with biological applications. Benjamin/Cummings, Menlo Park, ISBN 0-8053-5680-0.
- ^ Atkins P., de Paula J. (2006): Physical chemistry, 8th Ed. W. H. Freeman, San Francisco, ISBN 0-7167-8759-8
- ^ Whitten K.W., Gailey K. D. and Davis R. E. (1992): General chemistry, 4th Ed. Saunders College Publishing, Philadelphia, ISBN 0-03-072373-6.
- ^ Weast R. C., Ed. (1990): CRC Handbook of chemistry and physics. Chemical Rubber Publishing Company, Boca Raton, ISBN 0-8493-0470-9.
Vanjski linkovi
uredi- Java molecular orbital viewer shows orbitals of hydrogen molecular ion.
- The orbitron, a visualization of all atomic, and some molecular and hybrid orbitals
- xeo Visualizations of some atomic and molecular atoms
- OrbiMol Arhivirano 3. 3. 2014. na Wayback Machine Molecular orbital database.