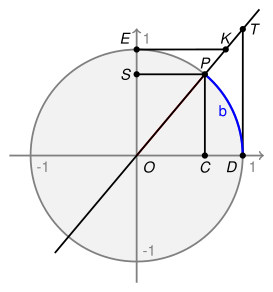
Grafik funkcije sekans Grafik funkcije kosekans
uredi
Sekans:
−
∞
<
x
<
+
∞
;
x
≠
(
n
+
1
2
)
⋅
π
;
n
∈
Z
{\displaystyle -\infty <x<+\infty \quad ;\quad x\neq \left(n+{\frac {1}{2}}\right)\cdot \pi \,;\,n\in \mathbb {Z} }
Kosekans:
−
∞
<
x
<
+
∞
;
x
≠
n
⋅
π
;
n
∈
Z
{\displaystyle -\infty <x<+\infty \quad ;\quad x\neq n\cdot \pi \ ;\,n\in \mathbb {Z} }
uredi
−
∞
<
f
(
x
)
≤
−
1
;
1
≤
f
(
x
)
<
+
∞
{\displaystyle -\infty <f(x)\leq -1\quad ;\quad 1\leq f(x)<+\infty }
Dužina perioda
2
⋅
π
:
f
(
x
+
2
π
)
=
f
(
x
)
{\displaystyle 2\cdot \pi \,:\,f(x+2\pi )=f(x)}
Sekans:
Osa simetrije:
f
(
x
)
=
f
(
−
x
)
{\displaystyle f(x)=f(-x)}
Kosekans:
Tačka simetrije:
f
(
−
x
)
=
−
f
(
x
)
{\displaystyle f(-x)=-f(x)}
Sekans:
x
=
(
n
+
1
2
)
⋅
π
;
n
∈
Z
{\displaystyle x=\left(n+{\frac {1}{2}}\right)\cdot \pi \,;\,n\in \mathbb {Z} }
Kosekans:
x
=
n
⋅
π
;
n
∈
Z
{\displaystyle x=n\cdot \pi \ ;\quad n\in \mathbb {Z} }
Sekans:
Minimum:
x
=
2
n
⋅
π
;
n
∈
Z
{\displaystyle x=2n\cdot \pi \,;\,n\in \mathbb {Z} }
Maksimum:
x
=
(
2
n
−
1
)
⋅
π
;
n
∈
Z
{\displaystyle x=(2n-1)\cdot \pi \ ;\,n\in \mathbb {Z} }
Kosekans:
Minimum:
x
=
(
2
n
+
1
2
)
⋅
π
;
n
∈
Z
{\displaystyle x=\left(2n+{\frac {1}{2}}\right)\cdot \pi \ ;\,n\in \mathbb {Z} }
Maksimum:
x
=
(
2
n
−
1
2
)
⋅
π
;
n
∈
Z
{\displaystyle x=\left(2n-{\frac {1}{2}}\right)\cdot \pi \ ;\,n\in \mathbb {Z} }
Nijedna funkcija nema nula.
Nijedna funkcija nema horizontalnih asimptota .
Nijedna funkcija nema prekida.
Nijedna funkcija nema prevojnih tačaka.
Sekans:
U pola perioda dužine, npr.
x
∈
[
0
,
π
]
{\displaystyle x\in [0,\pi ]}
Kosekans
U pola perioda dužine, npr.
x
∈
[
−
π
2
,
π
2
]
{\displaystyle x\in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}
Sekans:
sec
(
x
)
=
4
π
∑
k
=
0
∞
(
−
1
)
k
(
2
k
+
1
)
(
2
k
+
1
)
2
π
2
−
4
x
2
{\displaystyle \sec(x)=4\pi \,\sum _{k=0}^{\infty }{\frac {(-1)^{k}(2k+1)}{(2k+1)^{2}\pi ^{2}-4x^{2}}}}
Kosekans:
csc
(
x
)
=
1
x
−
2
x
∑
k
=
1
∞
(
−
1
)
k
k
2
π
2
−
x
2
=
∑
k
=
−
∞
∞
(
−
1
)
k
x
x
2
−
k
2
π
2
{\displaystyle \csc(x)={\frac {1}{x}}-2x\,\sum _{k=1}^{\infty }{\frac {(-1)^{k}}{k^{2}\pi ^{2}-x^{2}}}=\sum _{k=-\infty }^{\infty }{\frac {(-1)^{k}\,x}{x^{2}-k^{2}\pi ^{2}}}}
Sekans:
d
d
x
sec
(
x
)
=
sec
(
x
)
⋅
tan
(
x
)
=
sec
2
(
x
)
csc
(
x
)
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\sec(x)=\sec(x)\cdot \tan(x)={\frac {\sec ^{2}(x)}{\csc(x)}}}
Kosekans
d
d
x
csc
(
x
)
=
d
d
x
1
sin
(
x
)
=
−
csc
(
x
)
⋅
cot
(
x
)
=
−
csc
2
(
x
)
sec
(
x
)
=
−
cos
(
x
)
sin
2
(
x
)
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\csc(x)={\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {1}{\sin(x)}}=-\csc(x)\cdot \cot(x)=-{\frac {\csc ^{2}(x)}{\sec(x)}}=-{\frac {\cos(x)}{\sin ^{2}(x)}}}
Sekans:
∫
sec
(
x
)
d
x
=
ln
|
1
+
sin
(
x
)
cos
(
x
)
|
=
ln
|
sec
(
x
)
+
tan
(
x
)
|
{\displaystyle \int \sec(x)\,\mathrm {d} x=\ln \left|{\frac {1+\sin(x)}{\cos(x)}}\right|=\ln {\Big |}\sec(x)+\tan(x){\Big |}}
Kosekans
∫
csc
(
x
)
d
x
=
ln
|
sin
(
x
)
1
+
cos
(
x
)
|
=
ln
|
tan
(
x
2
)
|
{\displaystyle \int \csc(x)\,\mathrm {d} x=\ln \left|{\frac {\sin(x)}{1+\cos(x)}}\right|=\ln \left|\tan \left({\frac {x}{2}}\right)\right|}
Kompleksni argumenti
uredi
^ Konstantin A. Semendjajew: Taschenbuch der Mathematik
![{\displaystyle x\in [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49dc087a4edaa359c2dbf3c9064e1370e6782934)
![{\displaystyle x\in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1456d52196a1482372d7760aa863f111d53aa824)
