Apsolutna vrijednost

U matematici, apsolutna vrijednost je njegova brojna vrijednost i pri tom se ne uzima predznak broja .

Grafik apsolutne vrijednosti funkcije za realne brojeve.

Apsolutna vrijednost broja može se smatrati udaljenosti od nule.

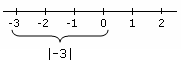
Apsolutna vrijednost |x| realnog broja x je maksimalni element para {x,-x}, koga sačinjavaju broj x i njemu suprotan broj -x. Dakle |-3|=3 jer je 3>-3; |x|=-x ako je -x>x, ili ekvivalentno ako je x<0; |x|=x ako je $x>-x, ili ekvivalentno ako je x>0; |x|=0 tada i samo tada kada je x=0.

Primjer

Brojevi 3 i -3 imaju istu apsolutnu vrijednost 3 .

Definicija

za bilo koji realan broj a apsolutna vrijednost |a| je jednaka broju a a ako je a ≥ 0, i −a ako je a < 0. $|a|=\left\{{\begin{matrix}a,&a\geq 0\\-a,&a<0\end{matrix}}\right.$ apsolutna vrijednost uvijek je pozitivna tako |a| ne može biti manja od nule ili 0

Apsolutna vrijednost se može uzeti kao udaljenost datog broja od 0 na brojnoj osi.

Osobine

Apsolutna vrijednost broja a ima osobine :

1. |a| ≥ 0
2. |a| = 0 akko a = 0.
3. |ab| = |a||b|
4. |a/b| = |a| / |b| (ако је b ≠ 0)
5. |a+b| ≤ |a| + |b| ( nejednakost trougla )
6. |a−b| ≥ ||a| − |b||
7. $\left|a\right|={\sqrt {a^{2}}}$
8. |a| ≤ b akko −b ≤ a ≤ b
9. |a| ≥ b akko a ≤ −b ili b ≤ a

iz navedenog imamo :

|x − 3| ≤ 9

−9 ≤ x−3 ≤ 9

−6 ≤ x ≤ 12

Kompleksni brojevi

Apsolutna vrijednost kompleksnog broja z. Na slici sr vidi da z i njegov kompleksno konjugirani z imaju istu apsolutnu vrijednost.

Apsolutna vrijednost kompleksnog broja takođe se naziva i modul kompleksnog broja.

Za $z\in \mathbb {C}$ data je kao $|z|={\sqrt {z\,{\overline {z}}}}$, ( ${\overline {z}}$ konjugovana vrijednost broja $z$.

Kako je $z=x+y\,i$ za $a,b\in \mathbb {R}$, imamo

$|z|={\sqrt {x^{2}+y^{2}}}$.

Kada je kompleksni broj izražen u polarnom obliku.

$z=re^{i\theta }$

Za $r\geq 0$ i $\theta$ realno je

$|z|=r$.

$|z|={\sqrt {z\cdot {\overline {z}}}}$

$|z|\neq {\sqrt {z^{2}}}$.

Odnos prema funkciji znaka

$|x|=x\operatorname {sgn}(x)$

ili

$|x|\operatorname {sgn}(x)=x,$

za $x\neq 0$

$\operatorname {sgn}(x)={\frac {|x|}{x}}.$

Diferencijal

Apsolutna funkcija realne vrijednosti ima izvod za svaki $x\neq 0$, ali nije diferencijabilna na $x=0$.

${\frac {d|x|}{dx}}={\frac {x}{|x|}}={\begin{cases}-1&x<0\\1&x>0.\end{cases}}$

Integral

$\int |x|dx={\frac {x|x|}{2}}+C,$

Udaljenost

Euklidska udaljenost između dvije tačke $a=(a_{1},a_{2},\dots ,a_{n})$ i $b=(b_{1},b_{2},\dots ,b_{n})$ je

${\sqrt {\sum _{i=1}^{n}(a_{i}-b_{i})^{2}}}.$

$|a-b|={\sqrt {(a-b)^{2}}}.$

Ako su zadane tačke $a=a_{1}+ia_{2}$ i$b=b_{1}+ib_{2}$ imamo

$|a-b|$	$=|(a_{1}+ia_{2})-(b_{1}+ib_{2})|$
	$=|(a_{1}-b_{1})+i(a_{2}-b_{2})|$
	$={\sqrt {(a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}}}.$

Prava vrijednost funkcije $d$ na skupu X × X naziva se vrijednost (ili funkcija udaljenosti) na X, ako zadovoljava sljedeće četiri aksiome:

$d(a,b)\geq 0$

$d(a,b)=0\iff a=b$

$d(a,b)=d(b,a)$

$d(a,b)\leq d(a,c)+d(c,b)$

Apsolutna vrijednost vektora

Apsolutna vrijednost vektora $v=(x_{1},x_{2},...,x_{n})$ u Euklidskom prostoru $R^{n}$ data je kao

$\left|\mathbf {v} \right|={\sqrt {x_{1}^{2}+x_{2}^{2}+...+x_{n}^{2}}}$.

$|v|$ se može smatrati dužinom vektora $v$.

Izvori

1. Absolute value
2. absolute value
3. Absolute Value

Također pogledajte

• Apsolutna vrijednost (algebra)
• Valuacija (algebra)

Reference

• Nahin, Paul J.; An Imaginary Tale; Princeton University Press; (hardcover, 1998). ISBN 0-691-02795-1
• O'Connor, J.J. and Robertson, E.F.; "Jean Robert Argand"
• Schechter, Eric; Handbook of Analysis and Its Foundations, pp 259–263, "Absolute Values", Academic Press (1997) ISBN 0-12-622760-8

Vanjski linkovi

• Ovaj članak sadrži materijal o apsolutna vrijednost sa PlanetMath-a, koji je licenciran po GFDL-u.
• Eric W. Weisstein, Absolute Value na MathWorld-u.